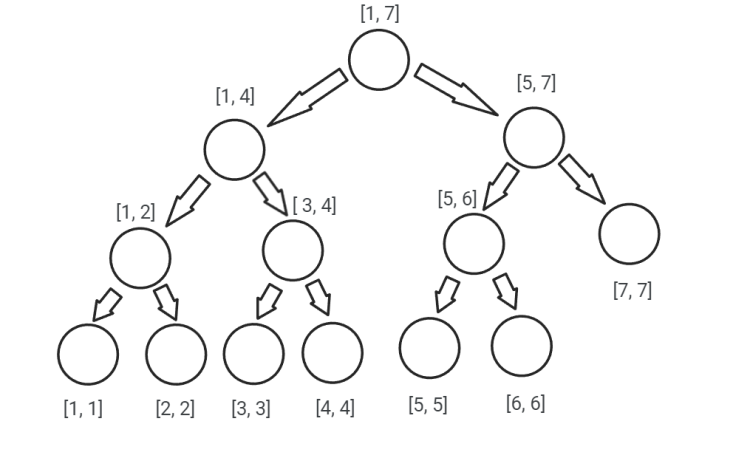
Un arbore de intervale este o structură de date similară cu un arbore binar, în care fiecare nod conţine informaţii despre un anumit interval dintr-un şir. La cazul general, un nod reține informații despre intervalul [st, dr]. Dacă intervalul asociat nodului are lungimea mai mare decât 1, nodului curent îi vor fi asociate alte două noduri ce vor descrie intervalele [st, mid] și [mid + 1, dr], unde mid = (st + dr) / 2.
Pentru a înțelege mai bine cum arată un astfel de arbore, vom considera șirul cu 7 elemente v = (4, 3, -1, 2, 9, 10, 6). Vrem să aflăm suma elementelor dintr-un anumit interval de poziții din șirul v. Arborele de intervale asociat lui v va fi:
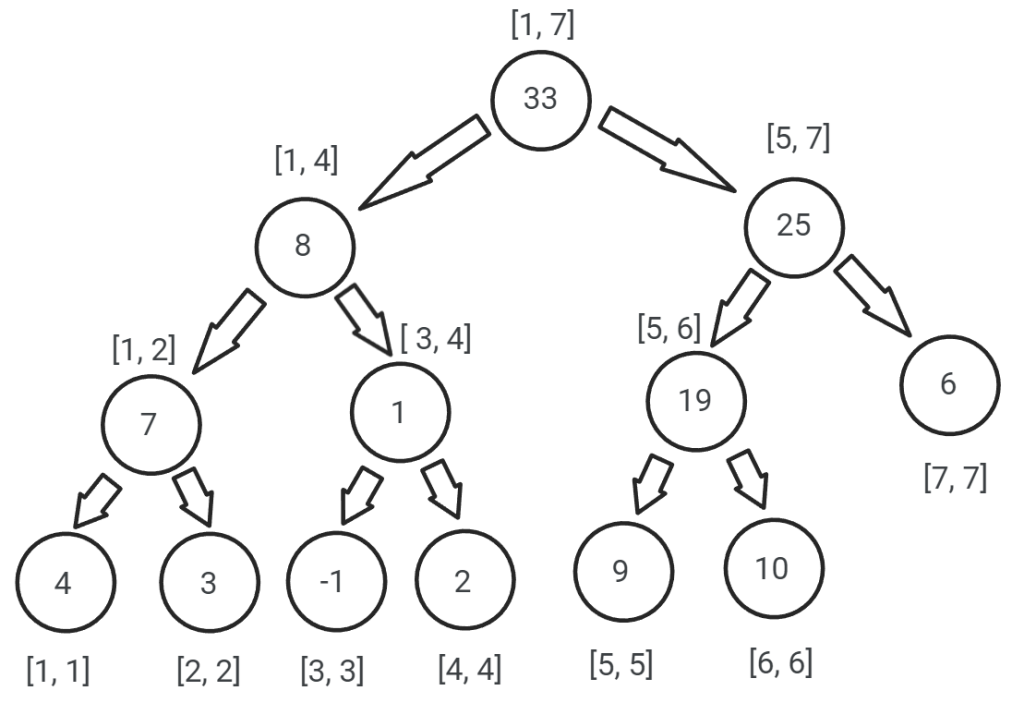
Vom construi arborele recursiv, folosind un vector. Dimensiunea vectorului va fi 4 * N, deoarece numărul de noduri este egal cu: 1 + 2 + 4 + … + 2^[log2(N)] < 2^([log2(N)] + 1) < 4 * N. Ulterior, vom vedea și ce operații putem face cu acest arbore.
Pentru a identifica nodurile, fiii nodului cu numărul k vor fi nodurile cu numerele 2 * k (pentru nodul din stânga), respectiv 2 * k + 1 (pentru nodul din dreapta). Rădăcina o vom numerota cu 1.
- Construirea arborelui de intervale în O(N)
Vom construi arborele recursiv, folosind următoarele observații:
a) dacă nodul curent descrie un interval cu un singur element, atunci el va lua valoarea din șir asociată poziției corespunzătoare;
b) dacă nodul curent descrie un interval cu mai multe elemente, atunci el va fi suma valorilor fiilor.
void build(int node, int st, int dr) {
if(st == dr) {
// nodul curent descrie un interval de lungime 1
tree[node] = v[st]; // preluăm valoarea din vector
return;
}
// împărțim intervalul curent în doua subintervale
int mid = (st + dr) / 2;
build(2 * node, st, mid); //mergem în nodul din stânga și construim primul subinterval
build(2 * node + 1, mid + 1, dr); // mergem în nodul din dreapta și construim al doilea subinterval
tree[node] = tree[2 * node] + tree[2 * node + 1]; // rezultatul pentru intervalul curent
}- Actualizarea unui element în O(log2(N))
Vom decide, pentru o poziție dată din șir, dacă ne mutăm în nodul din stânga sau dreapta, în funcție de subintervalele asociate nodurilor. În acest mod, vom ajunge să actualizăm rezultatele în timp logaritmic.
void update(int node, int st, int dr, int poz, int val){
if(st == dr){
// am ajuns în nodul corespunzător poziției care-și schimbă valoarea
tree[node] = val;
return;
}
int mid = (st + dr) / 2;
if(poz <= mid)
// dacă poziția pe care o cautăm se află în primul subinterval, vom merge în nodul corespunzător
update(2 * node, st, mid, poz, val);
if(poz > mid) // dacă poziția pe care o cautăm se află în al doilea subinterval, vom merge în nodul corespunzător
update(2 * node + 1, mid + 1, dr, poz, val);
tree[node] = tree[2 * node] + tree[2 * node + 1]; // refacem rezultatele din cauza modificării aduse
}Dacă vrem să modificăm, de exemplu, valoarea de la poziția 4, vom merge în nodurile:
- 1, care descrie intervalul [1, 7]
- 2, care descrie intervalul [1, 4]
- 5, care descrie intervalul [3, 4]
- 11, care descrie intervalul [4, 4], unde vom schimba valoarea asociata nodului cu parametrul val
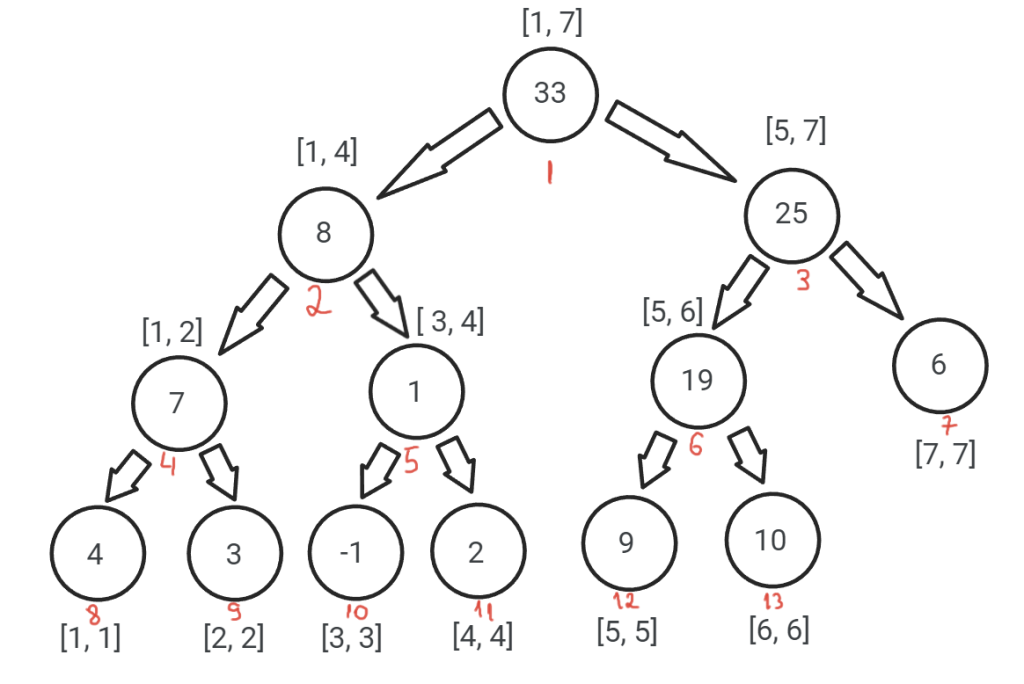
- Interogarea unui interval în O(log2(N))
Vom încerca să descompunem intervalul despre care dorim să-i aflăm suma în subintervale disjuncte din arbore. Formal, vom descompune un interval [x, y] în intervale de forma [x, y1], [y1 + 1, y2], [y2 + 1, y3], …, [yn + 1, y]. De exemplu, intervalul [2, 5] se descompune în: [2, 2], [3, 4], [5, 5]. Fiecare interval se va descompune în cel mult 2[log2(N)] intervale. Răspunsul interogării va fi suma valorilor din nodurile ale căror reuniune de intervale asociate dă exact intervalul [x, y].
int query(int node, int st, int dr, int x, int y){
if(x <= st && dr <= y) // mă aflu într-un subinterval care este inclus in intervalul de interogare( de exemplu, [3, 4] este inclus in [2,5])
return tree[node];
int mid = (st + dr) / 2, r1 = 0, r2 = 0;
if(x <= mid) // dacă mai există o porțiune din intervalul de interogare în primul subinterval, preiau rezultatul
r1 = query(2 * node, st, mid, x, y);
if(y > mid) // dacă mai există o porțiune din intervalul de interogare în al doilea subinterval, preiau rezultatul
r2 = query(2 * node + 1, mid + 1, dr, x, y);
return r1 + r2; // combin rezultatele
}Pentru intervalul de interogare [2, 5], avem:
- Nodul 1 cu intervalul [1, 7] care nu este inclus în [2, 5], deci îl vom împărți și verificăm dacă subintervalele rezultate se suprapun cu [2, 5]. Subintervalele sunt [1, 4] și [5, 7], deci vom merge în ambele, pe rând;
- Nodul 2 cu intervalul [1, 4] care nu este inclus în [2, 5], deci aplicăm același procedeu ca mai sus. Subintervalele sunt [1, 2] și [3, 4], deci, din nou, vom merge în ambele;
- Nodul 4 cu intervalul [1, 2] care nu este inclus în [2, 5]. Subintervalele sunt [1, 1] și [2, 2]. Decidem deci să mergem doar în intervalul [2, 2], fiind singurul care se suprapune cu [2, 5];
- Nodul 9 cu intervalul [2, 2]. Este un interval inclus în [2, 5], deci adunăm valorea din nod => 3;
- Revenim din [2, 2] în [1, 2], apoi în [1, 4] și mergem în nodul 5 cu intervalul asociat [3, 4], care este inclus în [2, 5], deci vom aduna valorea din nou => 1;
- Revenim din [3, 4] în [1, 4], pentru care rezultatul este 1 + 3 = 4 (suma elementelor intervalului rezultat din suprapunerea lui [2, 5] cu [1, 4]), apoi în [1, 7]. Mergem în nodul 3 cu intervalul asociat [5, 7], care nu este inclus în [2, 5]. Subintervalele sunt [5, 6] și [7, 7]. Singurul care se suprapune cu [2, 5] este [5, 6].
- Nodul 6 cu intervalul [5, 6] care nu este inclus în [2, 5]. Subintervalele sunt [5, 5] și [6, 6]. Decidem să mergem doar în intervalul [5, 5].
- Nodul 12 cu intervalul [5, 5] care este inclus în [2, 5], deci adunăm valorea din nod => 9;
- Revenim din [5, 5] în [5, 6], pentru care rezultatul este 9 (suma elementelor intervalului rezultat din suprapunerea lui [2, 5] cu [5, 6]), apoi în [5, 7] (cu același rezultat) și în final în [1, 7], pentru care avem rezultatul 4 + 9 = 13 (suma elementelor din [2, 5]).
- Actualizarea unui interval de elemente în O(log2(N))) – lazy update
Dacă dorim să actualizăm un anumit interval de elemente/poziții din vector, o abordare ca cea de mai sus ne va duce la o complexitate prea mare (este ineficient pentru un interval [x, y] pe care vrem să-l actualizăm cu o valoare val, să parcurgem fiecare poziție din acel interval). Ca urmare, vom folosi tehnica „lazy update”, care se referă la propagarea actualizărilor de la cele mai mari intervale incluse în [x, y] spre fiii lor, în jos. Pe lângă arborele de intervale principal, în care reținem rezultatele, vom construi un al doilea arbore de intervale care ne va ajuta să reținem cu ce valoare trebuie să actualizăm elementele din intervalul asociat unui nod. După ce actualizăm elementele, vom „propaga” valoarea de actualizare, reținută în al doilea arbore (ex: lazy[node]) către fii, adică lazy[2 * node], respectiv lazy[2 * node + 1], și vom pierde valoarea din lazy[node] (eliberăm lazy[node] de toate actualizările necesare intervalului pe care-l descrie „node”, întrucât le-am trimis fiilor lui).
Această operație poate fi vizualizată mai jos, unde este prezentat arborele de intervale lazy[], înainte și după propagarea valorii (adică 5) cu care trebuie actualizat intervalul [3, 4]:
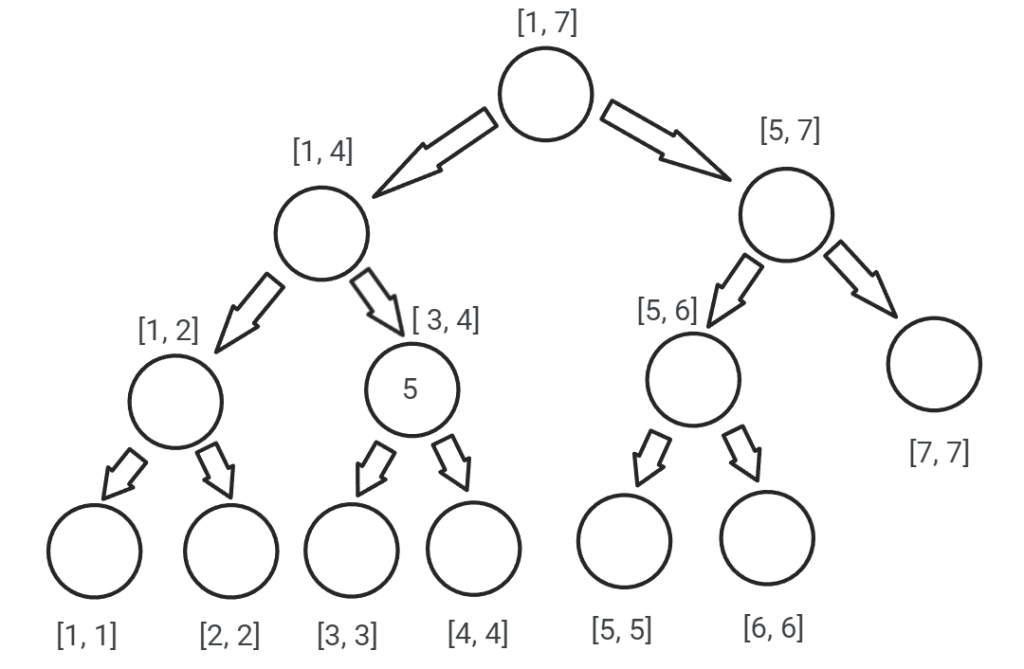
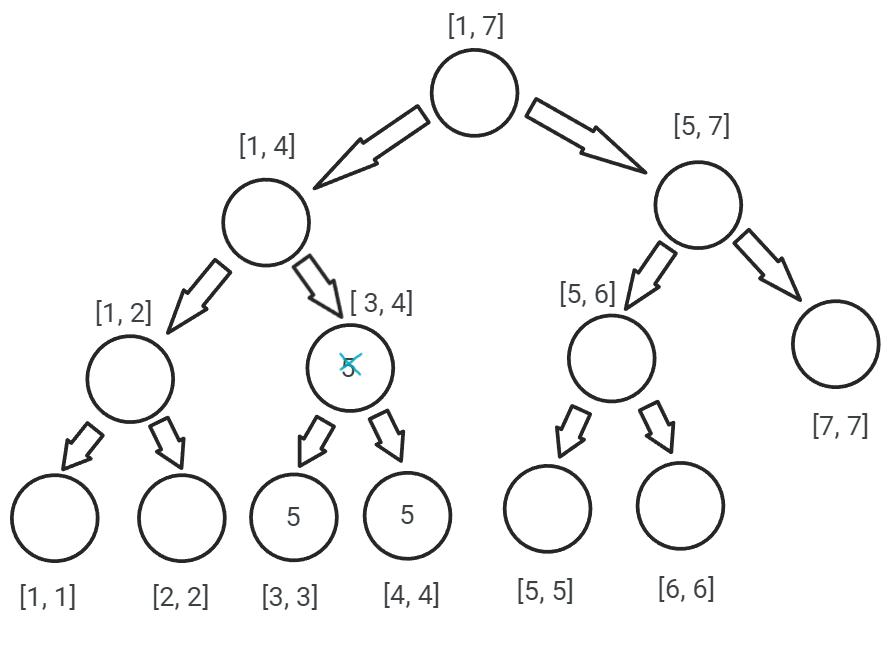
Funcția care ne ajută să actualizăm rezultatele folosind arborele lazy[] arată astfel:
void update_lazy(int node, int st, int dr){
// atenție! vectorul lazy[] trebuie inițializat în totalitate cu -1 înaintea efectuării oricărei operații pe arbore pentru a se păstra proprietatea de mai jos
if(lazy[node] == -1) // nu avem nimic de actualizat în intervalul curent (putem folosi o altă valoare care NU se află în intervalul valorilor posibile la actualizare)
return;
tree[node] = (dr - st + 1) * lazy[node]; // actualizăm rezultatele din nodul curent cu valoarea de actualizare * câte elemente sunt în interval, întrucât fiecare element se modifică
if(st != dr){ // există fii
// trimitem valoarea cu care actualizăm către fiii nodului curent
lazy[2 * node] = lazy[node];
lazy[2 * node + 1] = lazy[node];
}
lazy[node] = -1; // pierdem valoarea cu care actualizăm
}Ca urmare, funcția de actualizare va suferi modificări:
void update(int node, int st, int dr, int x, int y, int val){
// verificăm dacă trebuie să actualizăm intervalul curent cu o anumită valoare
update_lazy(node, st, dr);
if(x <= st && dr <= y){
// mă aflu într-un interval inclus în intervalul de actualizat (unul dintre intervalele de lungime maximă din arbore care este inclus în [x, y] - intervalul de actualizat)
lazy[node] = val; // modific cu actualizarea curentă
update_lazy(node, st, dr); // voi propaga actualizarea către fii
return;
}
int mid = ((st + dr) >> 1);
if(x <= mid)
update(2 * node, st, mid, x, y, val);
if(y > mid)
update(2 * node + 1, mid + 1, dr, x, y, val);
// acum vom propaga eventualele rezultate din fii către următoarele noduri
update_lazy(2 * node, st, mid);
update_lazy(2 * node + 1, mid + 1, dr);
tree[node] = tree[2 * node] + tree[2 * node + 1]; // refacem rezultatele
}ATENȚIE: după cum se observă, update_lazy() și update() sunt funcții diferite!
- update() ajută la actualizarea intervalelor de lungime maximă din arbore care sunt incluse în intervalul de actualizat;
- update_lazy() ajută la propagarea rezultatelor.
Interogările vor arăta un pic diferit: la fel ca funcția de actualizare, înainte să returnăm un rezultat dintr-un nod, verificăm dacă trebuie actualizat cu o anumită valoare.
int query(int node, int st, int dr, int x, int y){
// verificăm dacă este nevoie de actualizări ale rezultatelor
update_lazy(node, st, dr);
if(x <= st && dr <= y)
return tree[node];
int mid = (st + dr) / 2, r1 = 0, r2 = 0;
if(x <= mid)
r1 = query(2 * node, st, mid, x, y);
if(y > mid)
r2 = query(2 * node + 1, mid + 1, dr, x, y);
return r1 + r2;
}Autor: Pirnog Theodor Ioan
Colegiul Național „B. P. Hasdeu” Buzău