Al n-lea termen din șirul lui Fibonacci în timp logaritmic

Un termen din șirul lui Fibonacci se formează din suma ultimilor doi dinaintea lui, iar primii doi termeni îi considerăm 1. Șirul lui Fibonacci arată așa: 1 1 2 3 5 8 13 …

În acest articol vă voi prezenta 4 modalități de a afla al n-lea termen din șirul lui Fibonacci, de la cea mai ineficientă la cea mai eficientă. În continuare, vom nota al n-lea termen din șirul lui Fibonacci cu F(n).

Complexitate O(2ⁿ)
Complexitate O(n) recursiv
Complexitate O(n) nerecursiv
Complexitate O(log₂n)

1. Complexitate O(2ⁿ)

Știm că F(n) = F(n-1) + F(n-2). Să facem o funcție recursivă care să ne calculeze acest rezultat.

int fibo(int n)
{
   if (n <= 2)
      return 1;
   else
      return fibo(n-1) + fibo(n-2);
}

Dacă n este mai mic sau egal decât 2, atunci știm că rezultatul este 1 (pentru că F(1) = F(2) = 1).
Altfel, F(n) se obține din F(n-1) + F(n-2).

Să vedem de ce acest algoritm are complexitatea O(2ⁿ).

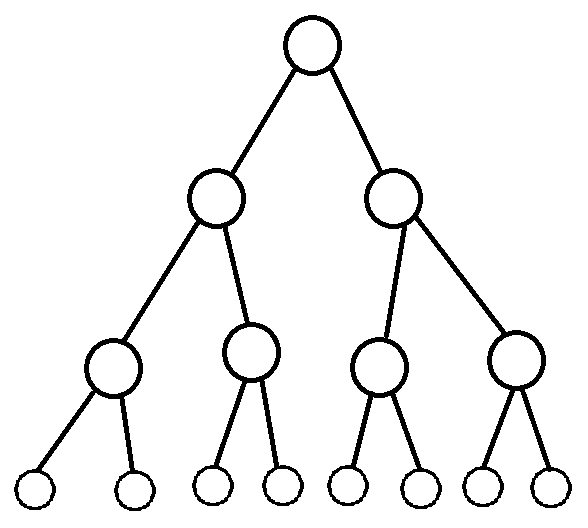
Fiecare cerculeț al acestui arbore îl vom considera a fi un apel de funcție.
Primul apel, F(n), este rădăcina acestui arbore.
F(n) face două apeluri, F(n-1) și F(n-2), adică cele de pe nivelul al doilea din acest arbore.
F(n-1) și F(n-2) fac fiecare câte două apeluri de funcție, deci se vor forma 4 în total (nivelul 3).
Din 4 apeluri, se mai fac alte 8 apeluri (nivelul 4).
Astfel, numărul total de apeluri va fi aproximativ 1 + 2 + 4 + 8 + … + 2^n-1, care înseamnă aproximativ 2ⁿ apeluri. Deci, complexitate de timp O(2ⁿ), iar complexitate de spațiu O(n).

2. Complexitate O(n) recursiv

Putem să îmbunătățim algoritmul de mai sus. Observăm că multe apeluri se calculează de foarte multe ori. De aceea, vom memora rezultatul unui apel cu scopul de a nu mai calcula tot apelul degeaba. Această soluție se mai numește și recursivitate cu memoizare.

int f[100];

int fibo(int n)
{
   if (n <= 2)
      return 1;
   else
   {
      if (f[n] != 0)
         return f[n];
      else
      {
         f[n] = fibo(n-1) + fibo(n-2);
         return f[n];
      }
   }
}

La fel ca la prima soluție, dacă n este mai mic sau egal decât 2, returnăm 1.
Altfel, verificăm dacă nu cumva am calculat deja F(n); dacă f[n] este diferit de 0, înseamnă că l-am calculat deja, și vom returna direct f[n], fără a mai face alte apeluri inutile.
Altfel (dacă f[n] este egal cu 0), înseamnă că nu l-am calculat pe F(n), deci vom face cele două apeluri F(n-1) și F(n-2), și vom însuma rezultatele în f[n], pentru a îl memora pentru alte apeluri.

3. Complexitate O(n) nerecursiv

Această soluție presupune folosirea programării dinamice. Codul este foarte simplu de înțeles, nu are rost să îl explic.

int f[100];

int fibo(int n)
{
   f[1] = f[2] = 1;
   for (int i = 3; i <= n; ++i)
      f[i] = f[i-1] + f[i-2];

   return f[n];
}

În general, ne mulțumim cu această complexitate. Codul este foarte ușor de scris și simplu de înțeles pentru oricine.

4. Complexitate O(log₂n)

Pentru a înțelege această soluție, trebuie să știm ce sunt matricele. Nu matricele din informatică, ci cele din matematică.

Din ce am înțeles eu, matricele sunt niște chestii inventate doar pentru a ușura calculele.
Există reguli diferite pentru adunarea, scăderea, înmulțirea și împărțirea matricilor, însă pe noi ne va interesa doar înmulțirea matricilor.

Înmulțirea matricelor 2×2 cu 2×2

$\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\times \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}= \begin{bmatrix} 1\times 5 + 2\times 7 & 1\times 6+2\times 8 \\ 3\times 5 + 4\times 7 & 3\times 6+4\times 8 \end{bmatrix}$

Înmulțirea matricelor 2×2 cu 2×1

$\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\times \begin{bmatrix} 5 \\ 6 \end{bmatrix}= \begin{bmatrix} 1\times 5 + 2\times 6 \\ 3\times 5 + 4\times 6 \end{bmatrix}$

Știind regulile de mai sus, putem să creăm următoarea ecuație:

$\begin{bmatrix} F(3) \\ F(2) \end{bmatrix}= \begin{bmatrix} 1&1 \\ 1&0 \end{bmatrix}\times \begin{bmatrix} F(2) \\ F(1) \end{bmatrix} \left ( 1 \right )$

Pentru a demonstra că ecuația de mai sus este adevărată, aceasta se traduce în:

$\begin{bmatrix} F(3) \\ F(2) \end{bmatrix}= \begin{bmatrix} 1\times F(2)+1\times F(1) \\ 1\times F(2)+0\times F(1) \end{bmatrix}$

Să formăm și ecuația pentru matricea formată din F(4) cu F(3):

$\begin{bmatrix} F(4) \\ F(3) \end{bmatrix}= \begin{bmatrix} 1&1 \\ 1&0 \end{bmatrix}\times \begin{bmatrix} F(3) \\ F(2) \end{bmatrix} \left (2 \right)$

Înlocuind ecuația (1) în ecuația (2), obținem:

$\begin{bmatrix} F(4) \\ F(3) \end{bmatrix}=\begin{bmatrix} 1&1 \\ 1&0 \end{bmatrix}\times \begin{bmatrix} 1&1 \\ 1&0 \end{bmatrix}\times \begin{bmatrix} F(2) \\ F(1) \end{bmatrix} =\begin{bmatrix} 1&1 \\ 1&0 \end{bmatrix}^{2}\times \begin{bmatrix} F(2) \\ F(1) \end{bmatrix}$

La cazul general:

$\begin{bmatrix} F(n) \\ F(n-1) \end{bmatrix}=\begin{bmatrix} 1&1 \\ 1&0 \end{bmatrix}^{n-2}\times \begin{bmatrix} F(2) \\ F(1) \end{bmatrix}$

O formă puțin mai simplificată este:

$\begin{bmatrix} F(n) \\ F(n-1) \end{bmatrix}=\begin{bmatrix} 1&1 \\ 1&0 \end{bmatrix}^{n-2}\times \begin{bmatrix} 1 \\ 1 \end{bmatrix}$

Singura problemă mai dificilă rămasă este ridicarea la putere a unei matrice. Pentru a obține complexitatea O(log₂n), vom folosi exponențierea rapidă. După, ne mai rămâne să înmulțim rezultatul cu încă o matrice. Acesta este codul:

struct mat2x2 {
   int v00, v01, v10, v11;
};

struct mat2x1 {
   int v00, v10;
};


mat2x2 multipl(mat2x2 a, mat2x2 b)
{
   mat2x2 c;
   c.v00 = a.v00 * b.v00 + a.v01 * b.v10;
   c.v01 = a.v00 * b.v01 + a.v01 * b.v11;
   c.v10 = a.v10 * b.v00 + a.v11 * b.v10;
   c.v11 = a.v10 * b.v01 + a.v11 * b.v11;

   return c;
}


mat2x1 multipl(mat2x2 a, mat2x1 b)
{
   mat2x1 c;
   c.v00 = a.v00 * b.v00 + a.v01 * b.v10;
   c.v10 = a.v10 * b.v00 + a.v11 * b.v10;

   return c;
}

mat2x2 pow(mat2x2 a, int exp)
{
   // initalizez ans cu a, si scad exp cu 1
   mat2x2 ans = a;
   exp--;

   while (exp != 0)
   {
      if (exp % 2 == 1)
      {
         ans = multipl(ans, a);
         exp -= 1;
      }
      else
      {
         a = multipl(a, a);
         exp /= 2;
      }
   }

   return ans;
}

int fibo(int n)
{
   if (n <= 2)
      return 1; // nu ridicam matricea la puterea 0 sau -1

   mat2x2 def1 = {1, 1, 1, 0};
   mat2x1 def2 = {1, 1};
   mat2x1 c = multipl(pow(def1, n-2), def2);

   return c.v00; // c.v00 e F(n), c.v10 e F(n-1)
}

Având în vedere că termenul al 46-lea este cel mai mare termen care poate fi calculat în tipul int (la toate cele 4 soluții prezentate), aceste soluții pot fi extinse pe numere mai mari folosind aritmetica modulară.

Îi mulțumesc indianului de pe YouTube și pbInfo-ului pentru că m-au învățat lucrurile pe care vi le-am prezentat.

Vă propun următoarele probleme de rezolvat: Fibonacci2, NumarDeSubmultimi1, kfib.