Fiind date două noduri p și q dintr-un arbore cu rădăcină, numim lowest common ancestor nodul de intersecție al lui p și q în drumul lor spre rădăcină.
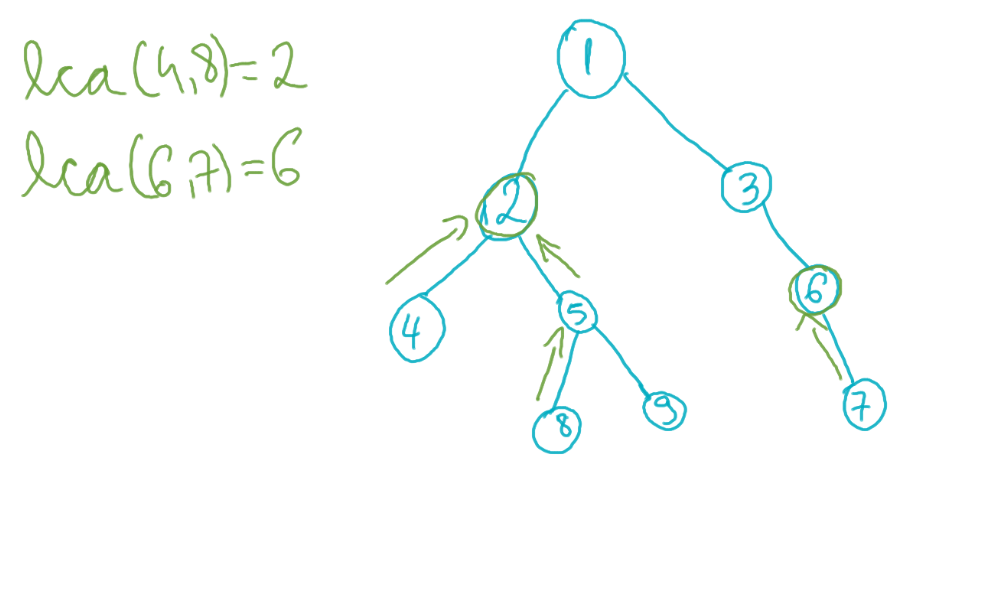
În acest arbore cu rădăcina în nodul 1, lca(4, 8) este 2, iar lca(6, 7) este chiar 6. La cazul general, lca(p, q), unde p și q sunt noduri ale arborelui, este primul strămoș comun al celor două noduri. Ca o mică observație, lca(p, q) poate fi chiar p sau q (exemplu: lca(6, 7) = 6).
Se pune problema determinării lca-ului într-un mod cât mai eficient. O primă variantă, care nu este foarte eficientă și care este mai greu de înțeles folosește noțiunea de binary lifting. Pentru a folosi ceea ce am prezentat în articolul anterior, ne vom concentra pe soluția cea mai eficientă, folosind euler’s tour.
Pentru început, să explicăm la ce se referă parcurgerea de tip euler a unui arbore. Vizual, ea poate fi văzută în felul următor:
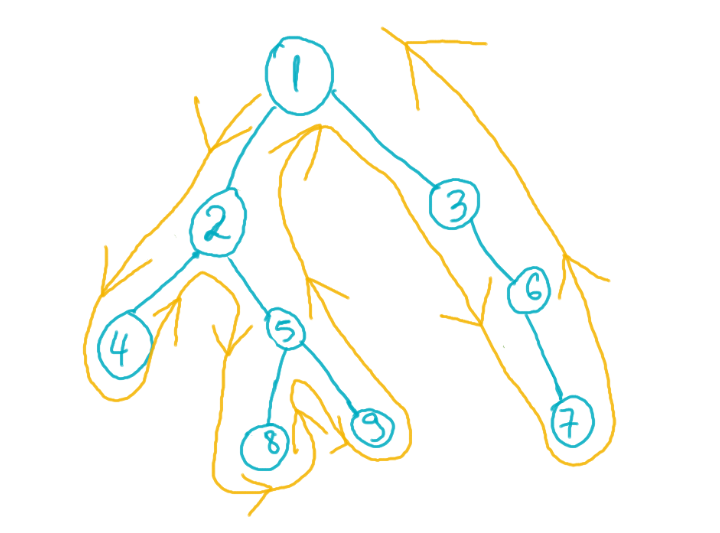
Acest tip de parcurgere ne poate ajuta să transformăm arborele într-un vector. Pe exemplul de mai jos, vectorul, să-l numim e[], arată astfel:
e[] = {1, 2, 4, 2, 5, 8, 5, 9, 5, 2, 1, 3, 6, 7, 6, 3, 1} Acest vector îl putem obține în urma unei simple parcurgeri DFS, astfel:
void dfs(int x){
e[++ne] = x;
for(auto y : fii[x]){
dfs(y);
e[++ne] = x;
}
}Dimensiunea vectorului e[] va fi exact 2 * numărul_de_noduri – 1 , deoarece trebuie să vizităm de două ori fiecare muchie a arborelui plus rădăcina arborelui.
Pentru a răspunde eficient la întrebările de genul „care este lca-ul nodurilor p și q„, vom avea nevoie de încă doi vectori, nivel[i] = nivelul pe care se află nodul i și poz[i] = prima apariție a nodului x în vectorul e[]. Așadar, noul DFS va arăta astfel:
void dfs(int x){
e[++ne] = x;
poz[x] = ne;
for(auto y : fii[x]){
nivel[y] = 1 + nivel[x];
dfs(y);
e[++ne] = x;
}
}Acum vom începe construirea matricei de dimensiune [log2(ne) + 1] * ne cu ajutorul căreia vom răspunde la fiecare query. Vom face aproximativ același lucru ca la algoritmul clasic de rmq, doar că trebuie să fim atenți să lucrăm cu noduri, adică prima liniei a matricei va fi chiar vectorul e[].
Secvența în care vom căuta răspunsul (nodul cu nivel minim) este delimitată de prima apariție a nodului p în e[] și prima apariție a nodului q în e[].
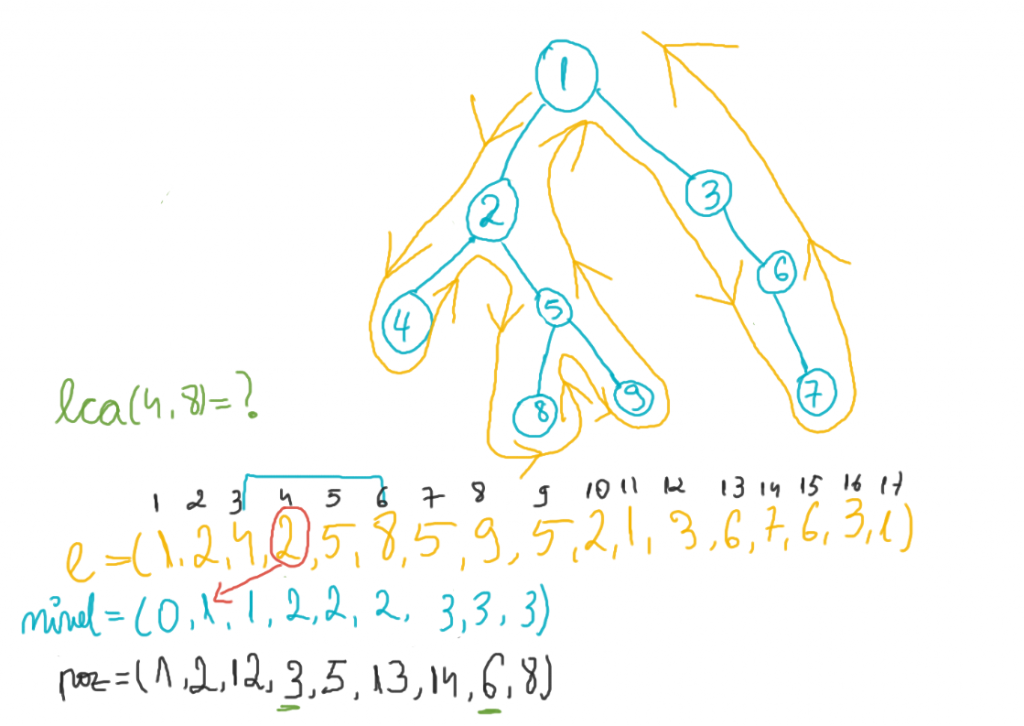
Pe acest exemplu, dintre nodurile 4, 2, 5, 8, nodul 2 se află pe nivelul minim.
Fie r[i][j] = nodul care se află pe nivelul minim în arbore, din secvența de lungime 2^i care se termină pe poziția j, din vectorul e[]
Vom construi simultan cu prima liniei a matricei și vectorul lg2[i] = [log2(i)], de dimensiune 2 * numărul_de_noduri – 1:
lg2[0] = -1; // pentru ca lg2[1] = 1 + lg2[0], adică 0
for(int i = 1; i <= ne; i++){
lg2[i] = 1 + lg2[i >> 1];
r[0][i] = e[i];
}Pentru restul matricei, vom aborda o tehnică similară algoritmului clasic de rmq, unde, pentru o secvență care se termină pe poziția j și are lungimea 2^i, vom compara nivelele pe care se află nodurile de nivel minim din cele două secvențe de lungime 2^(i – 1), care, intersectate sau nu, formează secvența curentă, adică r[i – 1][j] și r[i – 1][j – p], unde p = 1 << (i – 1):
for(int i = 1; (1 << i) <= ne; i++){
for(int j = (1 << i); j <= ne; j++){
r[i][j] = r[i - 1][j]; // presupunere inițială
int p = (1 << (i - 1));
if(nivel[r[i - 1][j - p]] < nivel[r[i - 1][j]]) // în caz contrar
r[i][j] = r[i - 1][j - p];
}
}Ne mai rămâne așadar să răspundem la întrebările de forma „care este lca-ul nodurilor p și q?”. Așa cum am spus mai devreme, vom căuta în secvența delimitată de prima apariție a nodului p și cea a nodului q, din e[], nodul cu nivel minim:
int lca(int x, int y){
// pentru a înțelege mai bine, se recomandă citirea articolului despre rmq
int st = poz[x], dr = poz[y]; // secvența din vectorul e
if(st > dr)
swap(st, dr);
int l = lg2[dr - st + 1]; // similar rmq clasic
int p = (1 << l); // similar rmq clasic
x = r[l][st + p - 1];
y = r[l][dr];
if(nivel[x] > nivel[y]) // comparăm nodurile de nivel minim din fiecare secvență
x = y;
return x;
}Autor: Pirnog Theodor Ioan
Colegiul Național „B. P. Hasdeu”, Buzău
