Problema satisfiabilității, prescurtată cu SAT (satisfiability), presupune existența unei atribuiri satisfiabile pentru o expresie booleană. O atribuire de valori booleene pentru o expresie se numește „atribuire satisfiabilă” dacă rezultatul expresiei, după atribuirea valorilor, este „adevărat”. De exemplu, expresia (x1 -> x2) ∧ (~x3 -> x4) este satisfiabilă, pentru x1 =1, x2 = 1, x3 = 0, x4 = 1.
Folosind următoarele echivalențe logice, o expresie poate fi simplificată pentru a obține forma normal conjunctivă, adică o conjuncție („∧” = AND gate) de propoziții în care fiecare propoziție este o disjuncție („∨” = OR gate) de literali. Deci, expresia de mai sus poate fi transformată în: (~x1 ∨ x2) ∧ (x3 ∨ x4).
Așadar, este suficient să studiem doar forma normal conjunctivă. În continuare, vom rezolva problema clasică de pe infoarena.
Vom pleca de la următoarea informație: x ∨ y = (~x -> y) ∧ (~y -> x) și de la tabelul pentru implicație, care arată în felul următor:
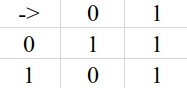
Deoarece forma normal conjunctivă, pe care noi o analizăm, este formată din conjucții de propoziții și dorim ca rezultatul expresiei să fie „adevărat”, fiecare dintre aceste propoziții (disjuncții de literari) trebuie să fie la rândul ei adevărată. Pentru ca o propoziție de forma x ∨ y să fie adevărată, trebuie ca (~x -> y) ∧ (~y -> x) (forma echivalentă de mai sus) să fie adevărată. Vom trata implicația ca fiind o muchie într-un graf orientat de la ~x la y, respectiv de la ~y la x. Scopul este să arătăm că ~x NU este accesibil din x, deci să NU existe drum de la x la ~x, adică x și ~x să NU facă parte din aceeași componentă tare conexă. Dorim să demonstrăm acest lucru datorită tabelului de implicație. Dacă ~x ar fi accesibil din x, ar însemna că x implică ~x, iar pentru x = 1, acest lucru se traduce prin „1 implică (->) 0”, lucru fals.
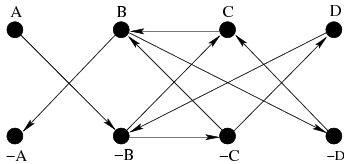
Convenție: pentru un nod x (1 ≤ x ≤ n), ~x va fi echivalat cu x + n (n + 1 ≤ ~x ≤ 2 * n). Prin urmare, când vom citi datele de intrare, nodurile cu „-” în față le vom transforma în -x + n. De exemplu, dacă x = –5, acesta înseamnă ~5, care, conform convenției, devine -(-5) + n = 5 + n.
Ca să determinăm dacă doua noduri fac parte din aceeași componentă tare conexă, vom păstra într-un vector comp[x] = componenta tare conexă din care face parte nodul x și folosim algoritmul lui Sharir-Kosaraju.
const int NMAX = 2e5;
vector <int> g[NMAX + 1], rg[NMAX + 1], topsort; // "g" = graful original, "rg" = graful transpus
int comp[NMAX + 1], n, ctc;
bitset <NMAX + 1> viz;
int val_asoc(int x){
// deoarece -x corespunde lui ~x, iar noi negăm un x (<= n) cu x + n, x (< 0) devine echivalent cu -x + n
if(x < 0)
return -x + n;
return x;
}
int neg(int x){
// negăm x in funcție de valorea sa față de n
if(x <= n)
return x + n;
// ex: dacă x = -5 înseamnă ~5. El se va transforma din cauza negației în -(-5) + n = 5 + n, iar ~(~5) = 5, deci
// vom scădea n pentru a obține rezultatul 5
return x - n;
}
void dfs(int x){
viz[x] = 1;
for(auto &y : g[x])
if(!viz[y])
dfs(y);
topsort.push_back(x);
}
void dfs2(int x){
comp[x] = ctc;
for(auto &y : rg[x])
if(!comp[y])
dfs2(y);
}
int main(){
int m = 0;
cin >> n >> m;
for(int i = 0; i < m; i++){
int x = 0, y = 0;
cin >> x >> y;
x = val_asoc(x);
y = val_asoc(y);
g[neg(x)].push_back(y);
g[neg(y)].push_back(x);
rg[y].push_back(neg(x));
rg[x].push_back(neg(y));
}
for(int i = 1; i <= 2 * n; i++)
if(!viz[i])
dfs(i);
reverse(topsort.begin(), topsort.end());
for(auto &y : topsort){
if(comp[y])
continue;
ctc++;
dfs2(y);
}Observații importante:
- Dacă doi literali fac parte din aceeași componentă tare conexă, atunci ei vor avea aceeași valoare;
- Dacă există drum de la un nod x la un nod y, atunci comp[x] ≤ comp[y];
Odată construit vectorul comp[], vom verifica daca nodul x face parte din aceeași componentă tare conexă cu ~x, caz în care expresia nu este 2SAT.
bool _2sat = 1;
for(int i = 1; i <= n; i++)
if(comp[i] == comp[i + n]) // i + n = ~i
_2sat = 0;
if(_2sat == 0){
cout << "-1";
return 0;
}Ce ne mai rămâne de făcut este să atribuim valori literalilor. Pentru orice nod x, dacă comp[x] > comp[~x], atunci îl vom seta pe x = 1 și ~x = 0, sau, dacă comp[x] < comp[~x], setăm x = 0 și ~x = 1. (!)
De ce funcționează?
Vom demonstra că nu există 2 noduri x și y astfel încât x = 1, y = 0 și y să fie accesibil din x (de cazul în care x = 1 și să existe un drum de la x la ~x ne-am ocupat deja, verificând dacă acestea fac sau nu fac parte din aceeași componentă tare conexă). Presupunem că există o pereche (x, y) de astfel de noduri.
- (!) => dacă x = 1 => comp[x] > comp[~x];
- (!) => dacă y = 0 => comp[y] < comp[~y];
Dacă y este accesibil din x, atunci comp[x] ≤ comp[y] => comp[~x] < comp[x] ≤ comp[y] < comp[~y] (din toate cele 3 inegalități). Din moment ce există un drum de la x la y, atunci există și un drum de la ~y la ~x (dacă x -> y <=> ~y -> ~x), deci comp[~y] ≤ comp[~x] (relație datorată sortării topologice realizate de algoritmul lui Sharir-Kosaraju) – contrar cu ce am scris mai sus. Prin urmare, nu există 2 noduri x și y astfel încât x = 1, y = 0 și y să fie accesibil din x.
for(int i = 1; i <= n; i++)
if(comp[i] > comp[i + n])
cout << 1 << " ";
else
cout << 0 << " ";Autor: Pirnog Theodor Ioan
Colegiul Național „B. P. Hasdeu”, Buzău
